The credit for developing the concept of logarithms in the 17th century is given to a Scottish mathematician named John Napier and to the less known Swiss craftsman, Joost Bürgi. The first logarithmic tables were published in 1614. The advantage of using logarithms for multiplication is that the product of two numbers to be multiplied can be determined by adding the logarithms of the two numbers and looking up the result in a table of anti-logarithms. Division uses the same process except the logarithms are subtracted. Logarithms simplified and reduced the time for computations especially in astronomy, navigation, surveying, and engineering.
 
A quote by a prominent French scholar and mathematician, Pierre-Simon Laplace about Napier’s logarithms is: “. . .  by shortening the labours, doubled the life of the astronomer.”  While there is not a similar quote for land surveyors, it is likely by using logarithms surveyors had to spend only half as much time on calculations as before.
 
Even after the introduction of mechanical calculators, surveyors used logarithms – especially in the field – as mechanical calculators were heavy and cumbersome to pack on the survey line; a surveyor proficient in the use of logarithms could perform most routine calculations nearly as fast as a person using a mechanical calculator. It was not until the Curta was introduced in the early 1960s that the use of logarithms in the field declined. The Curta will be described in the next article on mechanical calculators.
 
The author recalls using logarithms for triangulation surveys for control for hydrographic survey work in 1963. When a newly-commissioned land surveyor bought a Curta that had just appeared on the market, he and the hydrographer, an older gentleman, competed against each other to see who could calculate faster. The surveyor, using the Curta using natural functions, finished the calculation slightly faster than the hydrographer using logarithms, but in his haste to finish first the young surveyor got the wrong answer. Nevertheless, logarithms were soon destined to antiquity.
 
A device using logarithms is the slide rule, which dates back to the seventeenth century. The same Edmund Gunter who introduced the Gunter’s chain devised the earliest known logarithmic rule, known as the Gunter’s scale or the Gunter. It aided seamen with nautical calculations. In 1632, another English mathematician, William Oughtred, designed the first linear slide rule, although the familiar inner sliding rule was invented by the English instrument-maker Robert Bissaker in 1654. As the results given by slide rules are only to two or three significant digits, its application to surveying was limited.

Chambers Mathematical Tables. Chambers first published a volume of mathematical tables in 1844. New editions were published over the years in much the same format. Besides containing logarithms and natural functions of numbers and trigonometric functions, this edition also contains numerous pages explaining the use of the tables. The date of this edition is not identified in the book, however handwritten inside the front cover is what appears to be the name ”P.F. Yairvoor” and the date “25/3/27”.  Also is written the name “G.Z. Pinder, ALS.” Pinder ALS #096. Pinder was president of the Alberta Land Surveyors’ Association in 1947 and was made an honorary life member in 1957.  G.Z. Pinder carried out many surveys in the Pincher Creek area in the late 1920s and the 1930s.

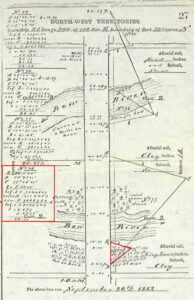
This field note page from an 1882 township outline survey by Charles F. Miles shows common calculations performed in the field by logarithms. In order to lay out 80 chains to the section corner, several distances across the Bow River channels were required. They were obtained by triangulation and calculation using trigonometry and logarithms. 

Slide rule used by Bill Wolley-Dod. He was president of the Alberta Land Surveyors’ Association in 1958 and was an honorary life member. He was active in the survey profession provincially, nationally, and internationally. After he retired from the firm of Wolley-Dod & MacCrimmon Surveys Ltd. in 1988, he served for a number of years as Inspector of Surveys for the Alberta Land Surveyors’ Association. The front of the slide rule is so worn that the graduations at the two ends are barely readable. The back of the scale rule shows common formulas and conversion factors. The centre slide can be reversed. Each scale is given a letter depending on its purpose. For example, for the scales shown on the back of the slide rule, B is for squares and square roots, K is for cube and cube roots, L for logs and C for multiplication and division. It is assumed that the worn out letters designating the scales on the front side of the slide rule include the trigonometric functions, for example S for sines and T for tangents.
Donated by Bill Wolley-Dod ALS #175
ALSA 2008.13.08
 
Sources of Information:

• Nature, Chambers Six-Figure Mathematical Tables, Website: https://www.nature.com/articles/163972b0
• Clark and Montelle, Logarithms: The Early History of a Familiar Function, Mathematical Association of America.
• Britannica Website: https://www.britannica.com/science/slide-rule
• Ron Manley’s Slide Rule site: http://www.sliderules.info/index.htm

Author: Gordon Olsson, ALS (Hon. Life) 
May 17, 2022
Copyright 2024 © Alberta Geomatics Historical Society